This blog contains answers to exercises set for students. While every effort is made to ensure that the information posted is correct, mistakes may occur from time to time.
Search This Blog
Thursday, December 18, 2014
Thursday, December 11, 2014
Wednesday, December 10, 2014
Friday, December 05, 2014
Tuesday, December 02, 2014
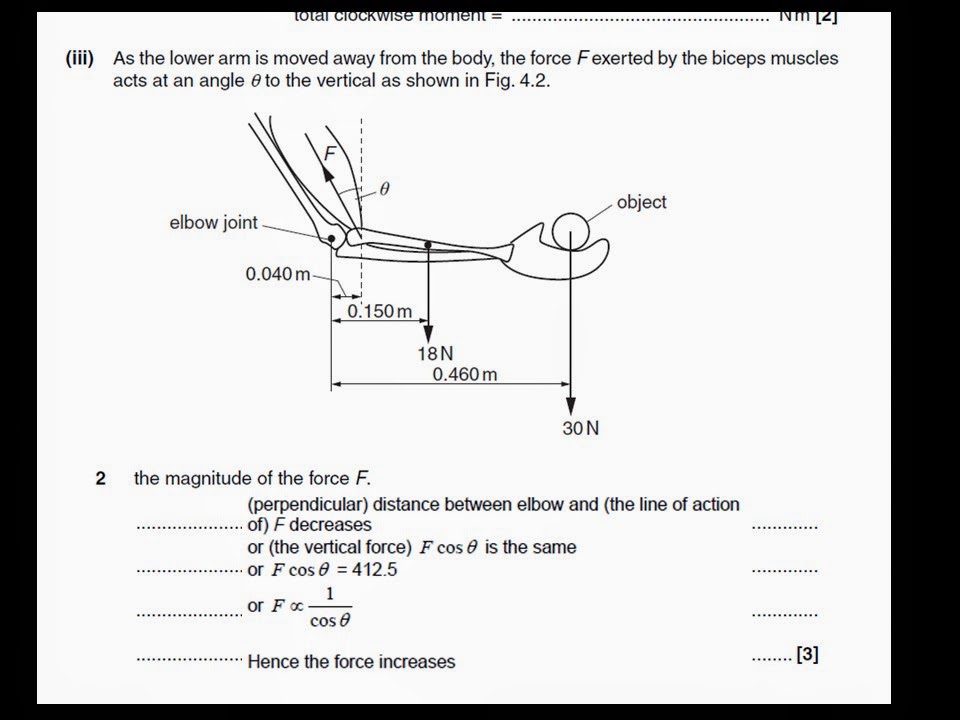
Monday, December 01, 2014
Young's Modulus - Past questions
(a) (i) Stress = force / area C1
force = stress ´ area
= 180 ´ 106 ´ 1.5 ´
10–4
= 27000 (N) A1
(ii) Y M = stress / strain C1
=
180 ´ 106 / 1.2 ´ 10–3 or using the gradient C1
=
1.5 ´ 1011 N m–2 A1
(b) brittle
elastic/
graph shown up to elastic limit
obeys
Hooke’s law / force α extension / stress α strain
no
plastic region B3
MAX
3
[8]
cast iron: brittle
brittle explained as having no plastic region
elastic
elastic explained as returning to original length when
the load is removed / linear graph / Hooke’s law obeyed
or equivalent words MAX 3
brittle explained as having no plastic region
elastic
elastic explained as returning to original length when
the load is removed / linear graph / Hooke’s law obeyed
or equivalent words MAX 3
copper: ductile
ductile explained as can be formed into a wire
initially elastic
plastic where it stretches more and more with little
increase in stress
plastic explained as does not return to its original length
when the load is removed
reference to necking at the end MAX 3
ductile explained as can be formed into a wire
initially elastic
plastic where it stretches more and more with little
increase in stress
plastic explained as does not return to its original length
when the load is removed
reference to necking at the end MAX 3
polythene: easy to deform / deformed with a small force
plastic
ductile
polymeric MAX 2
plastic
ductile
polymeric MAX 2
MAX
8
QWC: spelling, punctuation and grammar B1
organisation and logic B1
organisation and logic B1
[10]
Friday, November 28, 2014
Monday, November 24, 2014
Friday, November 21, 2014
Gravity questions
(a) arrow towards centre of planet 1
(b) (i) g
= GM/R2 1
(ii) gS/gO = R2/25R2; gS = 40/25 (= 1.6 N kg–1) 2
(iii) gC/gO = R2/16R2 giving gS = 40/16 (= 2.5 N kg–1) 1
(iv) average g = (2.5 + 1.6)/2 = 2.(05) (1)
Δp.e. (= mgavR) = 3.0 × 103 × 2.05 × 2.0 × 107; = 1.2 × 1011 (J) (2) 3
Δp.e. (= mgavR) = 3.0 × 103 × 2.05 × 2.0 × 107; = 1.2 × 1011 (J) (2) 3
(c) g
= v2/r; = 4π2(5R)/T2 (2)
1.6 = 4 × 9.87 × 1.0 × 108/T2 giving T2 = 24.7 × 108 and T = 5.0 × 104 (s) (2) 4
1.6 = 4 × 9.87 × 1.0 × 108/T2 giving T2 = 24.7 × 108 and T = 5.0 × 104 (s) (2) 4
[12]
Springs Questions
Q1
(a) One reading from the graph e.g. 1.0 N
causes 7 mm C1
Hence 5.0 (N)
causes 35 ±
0.5 (mm) A1
(allow
one mark for 35 ±
1 (mm)
(b) (i) Force
on each spring is 2.5 (N) C1
extension = 17.5
(mm) allow 18 (mm) or reading from graph A1
[allow
ecf from (a)]
(ii) strain energy = area under graph / ½ F ´ e C1
= 2 ´ 0.5 ´ 2.5 ´ 17.5 ´ 10–3
= 0.044 (J) A1
[allow
ecf from (b)(i)]
Q2
(a) (i) F
= kx / k is the gradient of the graph C1
k = 2.0 / 250 ´ 10–3 = 8.0 A1
Correct unit for
value given in (a)(i)
i.e.
0.008 or 8 ´
10–3 requires N mm–1.
Allow
N m–1 / kg s–2 if no working in (a)(i).
Do
not allow unit mark if incorrect physics in part (a)(i) B1
(ii) W = ½
(F ´
extension) / area under the graph C1
= ½
´ 2.0 ´ 0.250
= 0.25 (J) A1
(b) (i) F = 8 ´ 0.15 = 1.2 (N) A1
(ii) Hooke’s law continues to be obeyed / graph
continues as a straight
line
/ k is constant / elastic limit has not been reached B1
(c) (i) 1. correct
time marked on the graph with a V (t = 0.75 s or 1.75 s) B1
2. tangent in the correct place for downward
velocity or implied
by values B1
by values B1
value between 0.95 to 1.1(m s–1) A1
(ii) 1. X
marked in a correct place (maximum or minimum on graph) M1
2. relates the extension / compression to F
= kx to explain why the
force is a maximum or maximum
extension gives max force or
maximum extension gives max acceleration A1
maximum extension gives max acceleration A1
Q3
(a) The
extension of a spring is directly proportional to the applied force M1
as long as the elastic limit is not exceeded) A1
as long as the elastic limit is not exceeded) A1
(b) (i) Correct pair of values read from the graph
force constant = 12/0.080 C1
force constant = 150 (N m–1) A1
force constant = 12/0.080 C1
force constant = 150 (N m–1) A1
(ii) extension, x =  × 80 (= 133.33) (mm) C1
× 80 (= 133.33) (mm) C1
(E = ½ Fx)
energy = ½ × 2/ × 133.33 × 10–3
energy = 1.33 (J) A1
(E = ½ Fx)
energy = ½ × 2/ × 133.33 × 10–3
energy = 1.33 (J) A1
(iii) The
spring has not exceeded its elastic limit B1
(iv) (elastic potential energy = kinetic energy)
 M1
M1
m and k are constant, therefore x µ v. M1
m and k are constant, therefore x µ v. M1
Tuesday, November 04, 2014
Friday, October 17, 2014
Thursday, October 09, 2014
Y13 Circular Motion
(a) (i) speed
v = 2π r / t
v = 2 × π × 122/2 /(30 × 60) (1)
v = 0.21 m s–1 (1) allow 0.2 m s–1 2
v = 2 × π × 122/2 /(30 × 60) (1)
v = 0.21 m s–1 (1) allow 0.2 m s–1 2
(ii) F
= 12.5 kN × 16 = 200 kN (1) 1
(iii) W = F × s or
= 200 k × 2 × π × 122 / 2 (1) ecf (ii) allow ecf for distance from (i)
= 7.7 × 107 J (1) allow 8 × 107 2
= 200 k × 2 × π × 122 / 2 (1) ecf (ii) allow ecf for distance from (i)
= 7.7 × 107 J (1) allow 8 × 107 2
(iv) P
= W / t, energy / time or F × v or
= 7.67 × 107 / (30 × 60) (1) or ecf (iii) / (30 × 60)
= 42.6 kW (1) allow 43 kW, only allow 40 kW if working shown 2
= 7.67 × 107 / (30 × 60) (1) or ecf (iii) / (30 × 60)
= 42.6 kW (1) allow 43 kW, only allow 40 kW if working shown 2
(v) • Friction
force at bearing opposes motion so not useful (1)
• Friction force of tyres on rim drives wheel, so is useful (1)
• Electrical energy supplies power to drive wheels /
useful implied (1)
• Input energy (electrical or energy supplied to motor)
is converted into heat (1)
• Friction force of tyres on rim drives wheel, so is useful (1)
• Electrical energy supplies power to drive wheels /
useful implied (1)
• Input energy (electrical or energy supplied to motor)
is converted into heat (1)
Last point to do with the idea that
once moving with constant speed e.g.
• All work is done against friction
• No input energy is converted into Ek
• All input energy ends up as heat
• Any other relevant point relating to energy (1) 5
(b) (i) k = F / x• All work is done against friction
• No input energy is converted into Ek
• All input energy ends up as heat
• Any other relevant point relating to energy (1) 5
= 1.8 × 106 / 0.90 (1)
= 2.0 × 106 Nm–1 (1)
the
pendulum bob is travelling in a circle (1)
so it is accelerating towards the centre (1)
(it has a constant speed in the time interval just before vertical to just
after vertical)
so it is accelerating towards the centre (1)
(it has a constant speed in the time interval just before vertical to just
after vertical)
bob is not in equilibrium (1)
so the tension must be (slightly) larger than the weight of the bob (1) 3
so the tension must be (slightly) larger than the weight of the bob (1) 3
Friday, September 19, 2014
Monday, September 15, 2014
Monday, September 08, 2014
Markscheme for questions on circular motion
1. (i) (v = 2πr/t) t = 2π60/0.26 = 1450 s
Correct answer is 1449.96 hence allow 1.4 × 103
Do not allow a bare 1.5 × 103
Do not allow a bare 1.5 × 103
B1
(ii) correct substitution into F = mv2/r: eg F = (9.7 × 103 × 0.262)/60
C1
F = 10.9 N
Allow 11 N
A1
[3]
2. (i) THREE correct arrows at A, B and C all pointing towards
the centre (judged by eye)
the centre (judged by eye)
Ignore starting point of arrow
B1
(ii) 1. Greatest reaction force is at C
This is a mandatory M mark. The second mark cannot be gained unless this is scored.
M1
because it supports weight of sock AND provides the required
upward resultant (centripetal) force (WTTE)
upward resultant (centripetal) force (WTTE)
Any indication that candidates think that the centripetal force is a third force loses this second and possibly the next mark. They must make correct reference to the resultant force that provides the required centripetal force/acceleration.
A1
2. Least at A because sock’s weight provides part of the required
downward resultant (centripetal) force (WTTE)
downward resultant (centripetal) force (WTTE)
Allow answers using the equation F = mv2/r
such as Nc – mg (at C) = centripetal force OR mv2/r
OR mg +NA (at A) = centripetal force OR mv2/r
such as Nc – mg (at C) = centripetal force OR mv2/r
OR mg +NA (at A) = centripetal force OR mv2/r
B1
[4]
Friday, May 09, 2014
Thursday, May 08, 2014
Subscribe to:
Comments (Atom)